理論価格
相場が1,000円上昇したらオプションの価格はいくらになるのか?オプション価格は価格決定モデルを使って理論価格を算出することができます。この理論価格はボラティリティという変数により大きく左右されます。ここでは、ボラティリティ⇒価格決定モデル⇒理論価格という手順でオプションの理論の初歩を説明していきます。
ボラティリティ
原資産の価格の変動率のことで、年率(%)で表示されます。ボラティリティには過去の株価の変化をもとに統計的に算出される「ヒストリカル・ボラティリティ」と、市場参加者の取引価格から逆算される「インプライド・ボラティリティ」があります。オプションの理論価格ではインプライド・ボラティリティが利用されます。
インプライド・ボラティリティ
実際に取引されているオプション価格から算出された原資産の変動率(ボラティリティ)のことで、「予想変動率」ともいいます。これは重要な経済指標が大きく変わったり、政情不安が起きたりすると株価の変動を予想して大きくなります。オプション取引は「ボラティリティ取引」ともいわれるように、ボラティリティはオプションの価値を決める重要な尺度です。
ただ、変動率が高いというのは株価が特定の方向に動きやすいということを意味してはいません。通常、オプションの価格決定モデルは上下どちらの方向にも同じ程度の確率で変動することを前提としています。
ブラック-ショールズ・モデル(※)
プレミアムを算出するのに用いられる代表的なモデルで、考案した二人の人物(フィシャー・ブラック、マイロン・ショールズ)の名前が冠されています。オプションといえばこのモデルが連想されるほど一般化しています。原資産価格、権利行使価格、ボラティリティ、残存期間、金利、配当利回りの6つの値からオプションの理論価格を算出します。
以下ではブラック-ショールズ・モデルの数式を紹介します。

(※)ブラックーショールズ・モデルは現物を原資産とする現物オプション取引(日経225オプション取引、有価証券オプション取引等)のプレミアムの理論価格を算出するのに用いられます。一方、先物を原資産とする先物オプション取引(国債先物オプション取引、金先物取引等)についてはブラックモデルを用いるのが一般的です。
理論価格はボラティリティで決まる
ボラティリティが変わるとオプションの価格はどう変わるのか、日経平均株価15,000円、残存期間1か月の条件で、権利行使価格15,500円のコールの理論価格をグラフにしてみました。
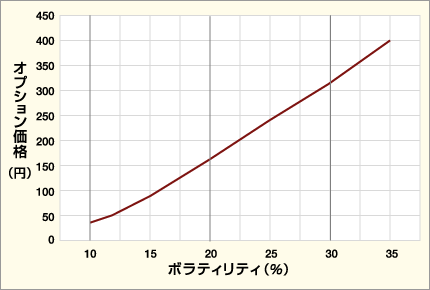
ボラティリティが上昇するということは、株価の変動幅がより大きくなることを意味しています。これによりオプションがイン・ザ・マネーになる可能性も高くなります。すなわち、ボラティリティが高いほどオプション価格も高くなり、逆にボラティリティが低いほどオプション価格も低くなります。
| ボラティリティ | オプションの売買 | オプション価格 |
|---|---|---|
| 高い | 買い手→権利行使の可能性が増加 売り手→リスクが増加 |
高い |
| 低い | 買い手→権利行使の可能性が低下 売り手→リスクが低下 |
低い |
リスク管理が最重要
オプション取引で最も重要なことはリスク管理です。市場の種々の変化(原資産価格の変化、満期までの残存期間の変化、ボラティリティの変化、金利の変化)によってオプション価格がどう変わるかを知ることが大切です。ここではリスクファクターと呼ばれる代表的な5つの指標を紹介します。
デルタ(Delta)
原資産の価格が動いたときに、オプション価格がどれだけ変化するかという感応度です。オプション価格は原資産の価格の影響を強く受けるので、デルタはリスク ファクターの中で最も重要です。デルタが0.6とは原資産が1動くとオプション価格は0.6(原資産の変化の60%)動くということです。具体的には日経平均株価が100円上昇するとそのオプションは60円上昇することを意味しています。デルタは深くITM(イン・ザ・マネー)になるほど±1に近づき、ATM(アット・ザ・マネー)で±0.5、OTM(アウト・オブ・ザ・マネー)ではゼロに近づきます。
| ITM | ATM | OTM | |
|---|---|---|---|
| コール買い プット売り |
+1に近づく | +0.5 | 0に近づく |
| プット買い コール売り |
-1に近づく | -0.5 | 0に近づく |
このデルタを利用してオプションのリスクを回避しようとする取引に、デルタ・ヘッジ取引があります。
ガンマ(Gamma)
原資産の価格が動いたときに、前述のデルタがどれだけ変化するかという指標です。ガンマが0.001とは原資産が1動くとデルタがその変化分の0.001増加するということです。具体的にはデルタ0.6、ガンマ0.001のオプションは日経平均株価が100円上昇するとデルタが0.7になることを意味しています。ガンマの値が大きいと原資産の変動でデルタが変わり易くなり、ヘッジ等の調整が頻繁に必要になります。ガンマはATM近辺で値が大きくなり、ITMおよびOTMになるほど0に近づきます。
| ITM | ATM | OTM | |
|---|---|---|---|
| コール買い プット買い |
0に近づく | +の最大 | 0に近づく |
| コール売り プット売り |
0に近づく | -の最大 | 0に近づく |
セータ(Theta)
満期までの残存時間の減少により、プレミアムがどれだけ減少するかという指標です。一般に残存期間が短くなるほど時間的価値の減少が大きくなり、セータの絶対値も大きくなります。
| ITM | ATM | OTM | |
|---|---|---|---|
| コール買い プット買い |
0に近づく | -の最大 | 0に近づく |
| コール売り プット売り |
0に近づく | +の最大 | 0に近づく |
ベガ(Vega)
ボラティリティ(予想変動率)が動いたときに、オプション価格がどれだけ変化するかという感応度です。ガンマの動きと似た傾向にありますが、原資産が動かなくてもボラティリティはいろいろな思惑から動くことがあります。
| ITM | ATM | OTM | |
|---|---|---|---|
| コール買い プット買い |
0に近づく | +の最大 | 0に近づく |
| コール売り プット売り |
0に近づく | -の最大 | 0に近づく |
ロー(Rho)
金利の変化によるオプション価格の変化の指標です。一般に短期金利1%の変化に対するオプション価格の変化で表します。リスク ファクターの中では比較的金利の与える影響は低く、特に残存期間の短いオプションではあまり考慮する必要がありません。

 初めての方
初めての方 メルマガ
メルマガ



